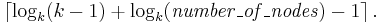K-ary tree

In graph theory, a k-ary tree is a rooted tree in which each node has no more than k children. It is also sometimes known as a k-way tree, an N-ary tree, or an M-ary tree.

A binary tree is the special case where k=2.

A full k-ary tree is a k-ary tree where within each level every node has either 0 or k children. A perfect k-ary tree is a k-ary tree in which all leaf nodes are at the same depth.^[1]

For a k-ary tree with height h, the upper bound for the maximum number of leaves is 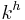$k^h$ . The total number of nodes is 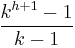$\frac{k^{h %2B 1} - 1}{k - 1}$ , while the height h is

$\left\lceil\log_k (k - 1) %2B \log_k (\mathit{number\_of\_nodes}) - 1\right\rceil.$

References

^ Black, Paul E. (20 April 2011). "perfect k-ary tree". U.S. National Institute of Standards and Technology. http://xlinux.nist.gov/dads/HTML/perfectKaryTree.html. Retrieved 10 October 2011.

Storer, James A. (2001). An Introduction to Data Structures and Algorithms. Birkhäuser Boston. ISBN 3764342536.

External links

N-ary trees, Bruno R. Preiss, P.Eng.